5. Sınıf Matematik Ders Kitabı Sayfa 292-293 Cevapları MEB Yayınları

5.Sınıf MEB Yayınları Matematik Ders Kitabı 292-293. Sayfa Cevapları Bölüm Sonu Değerlendirme
5. Sınıf Matematik Ders Kitabı Sayfa 292 Cevapları MEB Yayınları
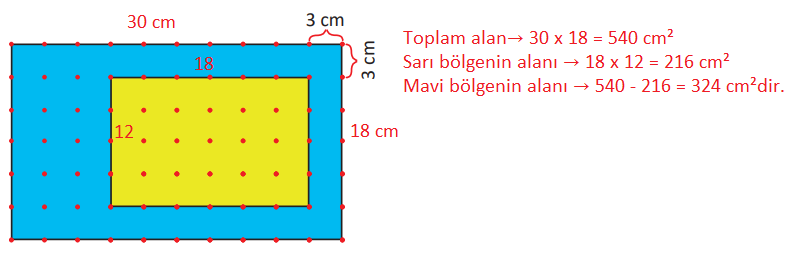
1) Noktalı kâğıt üzerinde verilen mavi boyalı alan ile sarı boyalı alan arasındaki fark kaç santimetrekaredir?
Cevap: D) 324
2) Kareli kâğıttaki şeklin çevresi 68 cm ise şeklin alanı kaç santimetrekare olur?
Cevap: A) 120


l. şekildeki dikdörtgen şeklindeki kumaş ortadan ikiye katlanarak ll. şekildeki kare elde ediliyor. ll. şekilden kare şeklinde kumaş parçası kesilip çıkarılıyor ve lll. şekil elde ediliyor. lll. şekildeki kumaşın çevresi 32 cm olduğuna göre l. şekildeki kumaşın alanı kaç santimetrekaredir?
Cevap: A) 128
3 şekil 32 cm olduğuna göre her kenarı
32 ÷ 4 = 8 cm’dir.
Her şekilde 8 cm kenar azaldığını düşünürsek;
II. Şekil → 32 x 2 = 64 cm
I. şekil → 64 x 2 = 128 cm olur.
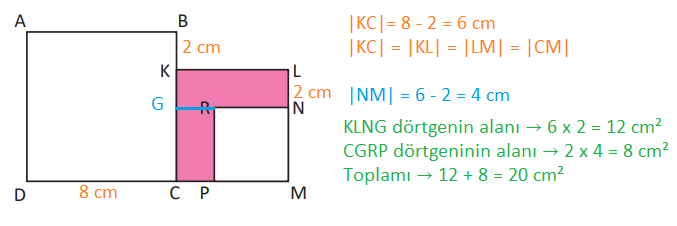
4) Yanda verilen şekilde ABCD, KLMC ve RNMP birer karedir. |DC| = 8 cm, |BK| = 2 cm ve |LN| = 2 cm olduğuna göre boyalı bölgenin alanı kaç santimetrekaredir?
Cevap: B) 20
5. Sınıf Matematik Ders Kitabı Sayfa 293 Cevapları MEB Yayınları
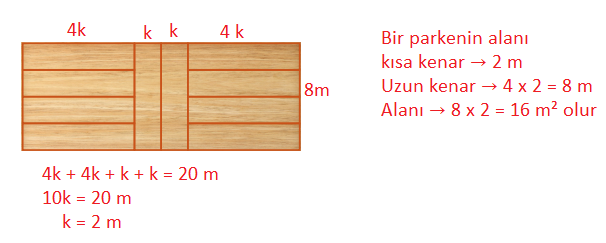
5) Yanda eş dikdörtgen şeklindeki parkelerle kaplanmış bir odanın zemini verilmiştir. Zeminin uzun kenarı 20 m olduğuna göre kullanılan dikdörtgen şeklindeki bir parça parkenin alanı kaç metrekaredir?
Cevap: A) 16
6) Bir kenar uzunluğu 8 m olan kare ile bir kenar uzunluğu 4 m olan dikdörtgenin alanları eşittir. Buna göre dikdörtgenin verilmeyen kenar uzunluğu kaç metredir?
Cevap: B) 16
Karenin alanı → 8 x 8 = 64 m²
Dikdörtgenin alanı →
y x 4 = 64
y = 64 ÷ 4
y = 16 m olur
7) Yanda verilen dikdörtgen şeklindeki halının üzerine bir masa yerleştirilmiştir. Masanın dikdörtgen şeklindeki üst yüzünün alanı, halının alanının %40’ı kadardır. Buna göre masanın üst yüzünün alanı kaç metrekaredir?
Cevap: C) 8

8) I. Alanı 72 cm² olan ve kenar uzunlukları santimetre cinsinden doğal sayı olan 6 farklı dikdörtgen çizilebilir.
II. Çevre uzunluğu 80 m olan karenin alanı 400 m² dir.
III. Alanı 90 cm² ve kenar uzunlukları santimetre cinsinden birer doğal sayı olan dikdörtgenin çevre uzunluğu 94 cm olabilir.
Yukarıda verilen ifadelerden hangisi ya da hangileri doğrudur?
Cevap: B) l ve ll
I. Alanı 72 cm² olan ve kenar uzunlukları santimetre cinsinden doğal sayı olan 6 farklı dikdörtgen çizilebilir.
1 x 72 = 72 cn²
2 x 36 = 72 cm²
3 x 24 = 72 cm²
4 x 18 = 72 cm²
6 x 12 = 72 cm²
8 x 9 = 72 cm² → 6 farklı dikdörtgen çizilebilir.
II. Çevre uzunluğu 80 m olan karenin alanı 400 m² dir.
80 ÷ 4 = 20 m her bir kenarı
Alanı → 20 x 20 = 400 m² olduğu için doğrudur.
III. Alanı 90 cm² ve kenar uzunlukları santimetre cinsinden birer doğal sayı olan dikdörtgenin çevre uzunluğu 94 cm olabilir.
1 x 90 = 90 cm² → 90 + 90 + 1 + 1 = 182 cm
2 x 45 = 90 cm² → 45 + 45 + 2 + 2 = 94 cm
3 x 30 = 90 cm² → 30 + 30 + 3 + 3 = 66 cm
5 x 18 = 90 cm² → 18 + 18 + 5 + 5 = 46 cm
6 x 5 = 90 cm² → 6 + 6 + 5 + 5 = 22 cm
9 x 10 = 90 cm² → 9 + 9 + 10 + 10 = 38 cm
(Hiçbiri uymadığı için yanlıştır)
9) KLMN dikdörtgeninin alanı 30 cm²dir. ABCD karesi, alanı KLMN dikdörtgeninin alanından büyük ve kenar uzunluğu santimetre cinsinden doğal sayı olan en küçük alanlı bir karedir. PRTS karesi, alanı KLMN dikdörtgeninin alanından küçük ve kenar uzunluğu santimetre cinsinden doğal sayı olan en büyük alanlı bir karedir. Buna göre ABCD ile PRTS karelerinin bir kenar uzunlukları toplamı kaç santimetredir?
Cevap: B) 11
KLMN dikdörtgeninin alanı 30 cm²dir.
ABCD karesinin alanı KLMN dikdörtgeninin alanından büyüktür. Buna göre karenin alanını 36 cm² olarak alabiliriz. Karenin bir kenarı 6 cm olur.
PRTS karesinin alanı KLMN dikdörtgeninin alanından küçüktür. Buna göre 5 . 5 = 25 cm² olarak alabiliriz. Karenin bir kenarı 5 cm olur.
5 + 6 = 11 cm olur.

