7. Sınıf Matematik Ders Kitabı 241-242-251-252. Sayfa Cevapları MEB Yayınları

7.Sınıf MEB Yayınları Matematik Ders Kitabı 241-242-251. Sayfa Cevapları Aritmetik Ortalama – Tepe Değer – Ortanca
7. Sınıf Matematik Ders Kitabı Sayfa 241 Cevapları MEB Yayınları
Hazır Mıyız?
7-A sınıfı öğrencilerinden Zeynep ve Rümeysa’nın ilk dönem matematik sınavlarından aldıkları puanlar şu şekildedir:
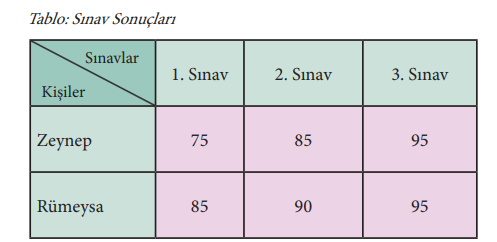
Yukarıdaki tabloda verilenlere göre aşağıdaki soruları cevaplandırınız.
1. Zeynep ve Rümeysa’nın aldıkları puanların aritmetik ortalamalarını ayrı ayrı hesaplayınız
Cevap:
Zeynep → 75 + 85 + 95 = 255
255 ÷ 3 =85
Rümeysa → 85 + 90 + 95 = 270
270 ÷ 3 = 90
2. Zeynep ve Rümeysa’nın aldıkları puanların açıklıklarını ayrı ayrı hesaplayınız
Cevap:
Zeynep → 95 – 75 = 20
Rümeysa → 95 – 85 = 10
3. Zeynep ve Rümeysa’nın başarı durumlarını karşılaştırınız.
Cevap: Aritmetik ortalamalara göre Rümeysa daha başarılıdır.
7. Sınıf Matematik Ders Kitabı Sayfa 242 Cevapları MEB Yayınları
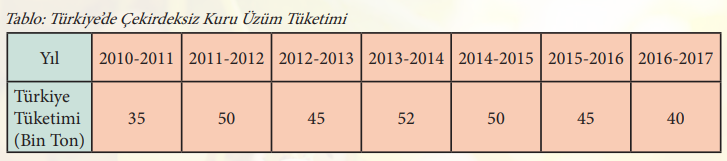
Yukarıdaki tabloda Türkiye’de tüketilen çekirdeksiz kuru üzüm miktarı verilmektedir. Tabloyu ve metinde verilen bilgileri dikkate alarak aşağıdaki soruları cevaplayınız.
➢ Türkiye’de yıllara göre ortalama kaç bin ton çekirdeksiz kuru üzüm tüketilmektedir?
Cevap:
35 + 50 + 45 + 52 + 50 + 45 + 40 = 317
317 ÷ 7 = 45,29
➢ Tabloya göre tüketilen çekirdeksiz kuru üzüm miktarlarından en çok tekrar eden değer hangisidir?
Cevap: En çok tekrar eden değer 45 ve 50’dir.
35 – 50 – 45 – 52 – 50 – 45 – 40
➢ Tüketilen çekirdeksiz kuru üzüm verilerini küçükten büyüğe veya büyükten küçüğe sıraladığımızda ortadaki miktarın değişip değişmediğini nasıl yorumlarsınız?
Cevap:
Küçükten büyüğe → 35 < 40 < 45 = 45 < 50 = 50 < 52
Büyükten küçüğe → 52 > 50 = 50 > 45 = 45 > 40 > 35
Ortadaki miktar değişmemiştir.
7. Sınıf Matematik Ders Kitabı Sayfa 251 Cevapları MEB Yayınları
SIRA SİZDE
1. Aşağıdaki boşluklara uygun ifadeleri yazınız.
Cevap:
a. Bir bütünün parçaları verilip bütün ile parçaları karşılaştırılmak isteniyorsa …..daire…. grafiği kullanılır.
b. Değerler gösterilirken ve veriler arasında karşılaştırma yapılırken …sütun… grafiği kullanılır.
c. Bir veri grubundaki verilerin belirli zaman aralığındaki değişimini (artış veya azalışını ) görmek için …çizgi… grafiği kullanılır.
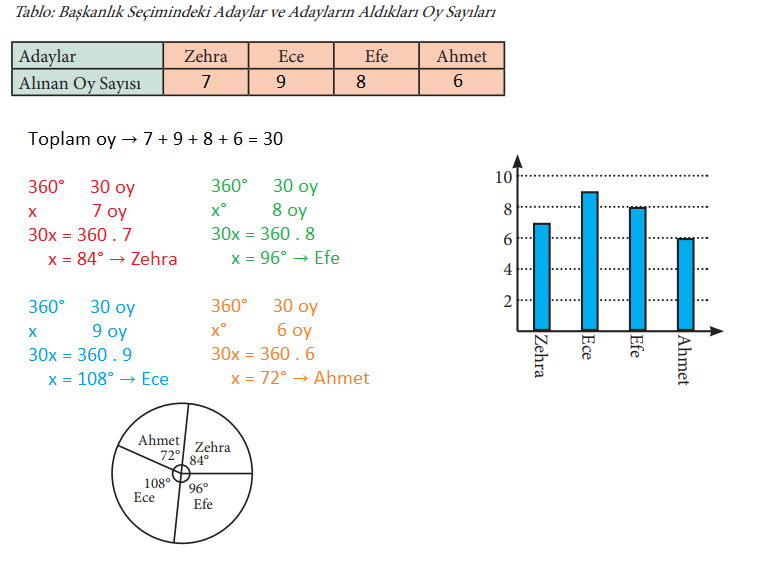
2. 7-H sınıfında yapılan başkanlık seçiminde Zehra 7, Ece 9, Efe 8, Ahmet 6 oy almıştır. Bu verilere ait sıklık tablosunu doldurunuz. Tablodan yararlanarak daire ve sütun grafiklerini oluşturunuz.
Cevap:
3. 4, 3, 8, 9, 14, 6, 4, 7, 9, 6 veri grubunun tepe değer, ortanca ve aritmetik ortalamasını bulunuz
Cevap:
3, 4, 4, 6, 6, 7, 8, 9, 9, 14
Tepe değer → 4, 6, 9
Ortanca → 6 + 7 = 13 → 13 ÷ 2 = 6,5 olur.
Aritmetik ortalama → 3 + 4 + 4 + 6 + 6 + 7 + 8 + 9 + 9 + 14 = 70
70 ÷ 10 = 7 olur
4. Yaşlarının aritmetik ortalaması 35 olan 4 kişilik bir gruba 45 yaşında biri katılırsa yeni ortalama kaç olur?
Cevap:
35 x 4 = 140
140 + 45 = 185
185 ÷ 5 = 37
5. Aşağıdaki ifadeleri inceleyiniz. İfadeler doğru ise “D”, yanlış ise “Y” yazınız
Cevap:
a. (..Y..) Bir veri grubunda ortanca bulunurken verilerin sıralaması önemli değildir.
→ Küçükten büyüğe sıralanması gerekir.
b. (..D..) Bir veri grubunun 4 tane tepe değeri olabilir.
c. (..Y..) Bir veri grubuna aritmetik ortalamadan daha büyük bir sayı eklenirse ortalama azalır.
→ Bir veri grubuna aritmetik ortalamadan daha büyük bir sayı eklenirse ortalama artar
ç. (..D..) Herhangi bir veri grubunun ortalaması, ortancası ve tepe değeri birbirine eşit olabilir.
d. (..D..) Veri adedi çift sayıda ise ortancayı bulmak için ortadaki iki sayının ortalaması alınır.
e. (..Y..) Bir veri grubunun her zaman tepe değeri mevcuttur.
→ Bir veri grubunun her zaman tepe değeri olmayabilir
f. (..Y..) Bir veri grubunda birden fazla ortanca bulunabilir
→ ortanca olan sayı çiftse toplanıp ikiye bölünür ve ortanca bulunur.
7.Sınıf MEB Yayınları Matematik Ders Kitabı 252. Sayfa Cevapları Kazanım Kavrama Testi – 21
7. Sınıf Matematik Ders Kitabı Sayfa 252 Cevapları MEB Yayınları
1. Türkiye’de en çok hangi renk araçların satıldığı konusunda araştırma yapan bir araştırmacının aşağıdaki veri analizi yöntemlerinden hangisini tercih etmesi daha uygun olur?
Cevap: C) Tepe değer
2. Yaş ortalaması 13 olan bir gruptan 12 yaşında olan biri çıktığına göre ortalama nasıl değişir?
Cevap: B) Artar.
Grup azalır yaş ortalamasından küçük biri çıktığı için ortalama artar.
3. 10, 7, 10, 10, 9, 8, 12 şeklinde verilen bir veri grubundan 12 çıkarılırsa hangisinde bir değişiklik olmaz?
Cevap: C) Tepe değer
7, 8, 9, 10, 10, 10, 12
Açıklık → 12 – 7 = 5
Ortanca → 10
Tepe değer → 10
Aritmetik ortalama → 7 + 8 + 9 + 10 + 10 + 10 + 12 = 66
66 ÷ 7 = 9,43
12 çıkarılırsa;
7, 8, 9, 10, 10, 10
Açıklık → 10 – 7 = 3
Ortanca → 10 + 9 = 19 → 19 ÷ 2 = 9,5
Tepe değer → 10
Aritmetik ortalama → 7 + 8 + 9 + 10 + 10 + 10 = 54
54 ÷ 6 = 9
Değişmeyen tek değer tepe değerdir.
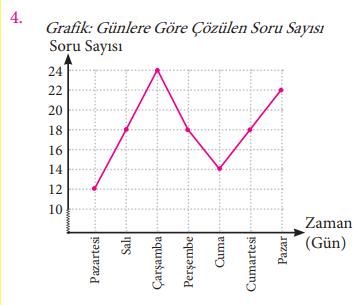
Yukarıda verilen grafik, İbrahim’in 1 hafta boyunca çözdüğü Türkçe soru sayısını göstermektedir. Buna göre aşağıdakilerden hangisi yanlıştır?
Cevap: D) Açıklık 18’dir.
12, 14, 18, 18, 18, 22, 24
Aritmetik ortalaması → 12 + 18 + 24 + 18 + 14 + 18 + 22 = 126
126 ÷ 7 = 18
Tepe değeri → 18
Ortanca → 18
Açıklık → 24 – 12 = 12
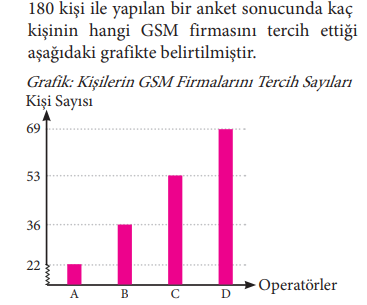
Yukarıdaki sütun grafiğinden yararlanarak bir daire grafiği oluşturulmak isteniyor. 5 ve 6. soruları bu verilere göre cevaplayınız.
5. A firmasını tercih eden kişi sayısına ait daire diliminin merkez açısının ölçüsü kaç derecedir?
Cevap: A) 44
360° 180 kişi
x° 22 kişi
180x = 360 . 22
x = 44° → A firması
6. D firmasını tercih eden kişi sayısına ait daire diliminin merkez açısının ölçüsü, C firmasını tercih eden kişi sayısına ait daire diliminin merkez açısının ölçüsünden kaç derece fazladır?
Cevap: C) 32
360° 180 kişi
x° 69 kişi
180x = 360 . 69
x = 138° → D firması
360° 180 kişi
x° 53 kişi
180x = 360 . 53
x = 106° → C firması
138 – 106 = 32 fazladır
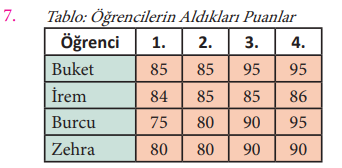
Yukarıdaki tabloda 4 öğrencinin sosyal bilgiler sınavlarında aldıkları puanlar verilmiştir. Buna göre en başarılı öğrenci kimdir?
Cevap: A) Buket
Aritmetik ortalaması en yüksek olan öğrenci en başarılı öğrencidir. Buna göre;
Buket → 85 + 85 + 95 + 95 = 360 → 360 ÷ 4 = 90
İrem → 84 + 85 + 85 + 86 = 340 → 340 ÷ 4 = 85
Burcu → 75 + 80 + 90 + 95 = 340 → 340 ÷ 4 = 85
Zehra → 80 + 80 + 90 + 90 = 340 → 340 ÷ 4 = 85
En başarılı öğrenci Buket’tir.





